Reinforcement Learning
Abstract
This Reinforcement Learning problem described in this article has the following pre-conditions:
- Multi-agent environment
- Continuous state
- Continuous action
- Incomplete observation
- Various initial states
- Sparse reward function
In simple terms, more than one player takes part in this game. Map is partially hidden from each player by the fog of war. Each of the players can observe an almost infinite number of options for events and at each moment can choose an action from a large set. Players can start the game on different maps, and the result is summed up only at the end of the game without intermediate results.
Among the shortcomings of such approaches, it is worth noting, that some research is conducted on special matches, with the significantly modified environment. For example, it may contain only a tactical component for the troops management and lack the economy, technology and production components. Some use the original environment, but economics, production, and technology are delegated to a specific algorithm, leaving only tactics for learning. Others, using the original environment, substitute the current set of actions with the designed combinations of actions, which they call macro actions, change the reward space, but training and testing are carried out in extremely biased conditions. Most of the articles are based on the professional players games’ recordings. AlphaStar by the DeepMind has been initially trained to a very high level on the game recordings, and only then the reinforcement learning based on the recorded games experience was added.
The biggest complexity of such a task is that, due to the presence of several agents, the trained agent must be able to adapt to the opponents’ actions, opposed to performing actions in the conditions of a fixed environment.
Matches are played on game maps. In addition to rivals, the map includes resources (minerals, gas), plateaus of different heights, transitions between plateaus, and airspaces. The match begins with each player being given a main base and 12 workers. The goal is to destroy all the buildings of the opponent. To do this, you need to collect resources, improve the economy, create production, hire troops, develop technology, and give battles.
There are three species in the game. Each having own technological tree. Protoss species has been chosen for this training. The bot will be trained to play FOR this species, and, in order for it to have the option to play with itself, it will also learn to play AGAINST the Protoss species.
Challenge
At each point of time, the environment generates an observation for each player, taking into account the fog of war. Observation consists of a sequence of statistics for each visible unit on the map, a screen, a minimap, general statistics such as the number of resources, the limit of the army, etc. Every agent generates an action upon the observation.
Actions can be of the following types:
- Without an actor: global actions that do not require units;
- Fast: actions that unit performs without additional parameters;
- Precise: actions that unit performs indicating the the coordinates on the map;
- Target: the targeted unit actions.
For each of these actions, you need to generate your own set of parameters. It was decided to generate only the action type for the faster training; parameters are selected using a simple heuristic.
In reinforcement learning, you need to reward the agent for the actions performed. The agent, in turn, tries to maximize the reward. The default reward within the environment is +1, 0, -1 at the end of the trajectory for a win, draw, and loss respectively. A time limit was set to 21 minutes.25 seconds, or 2881 steps for training purposes. A draw is recognized if the match has not been finished within the defined time limit.
The Exploring Problem
There's a problem, that some of the actions are located up the technology tree, as shown in the figure. To perform such an action, you first need to walk up the tree, successfully performing a certain set of actions.
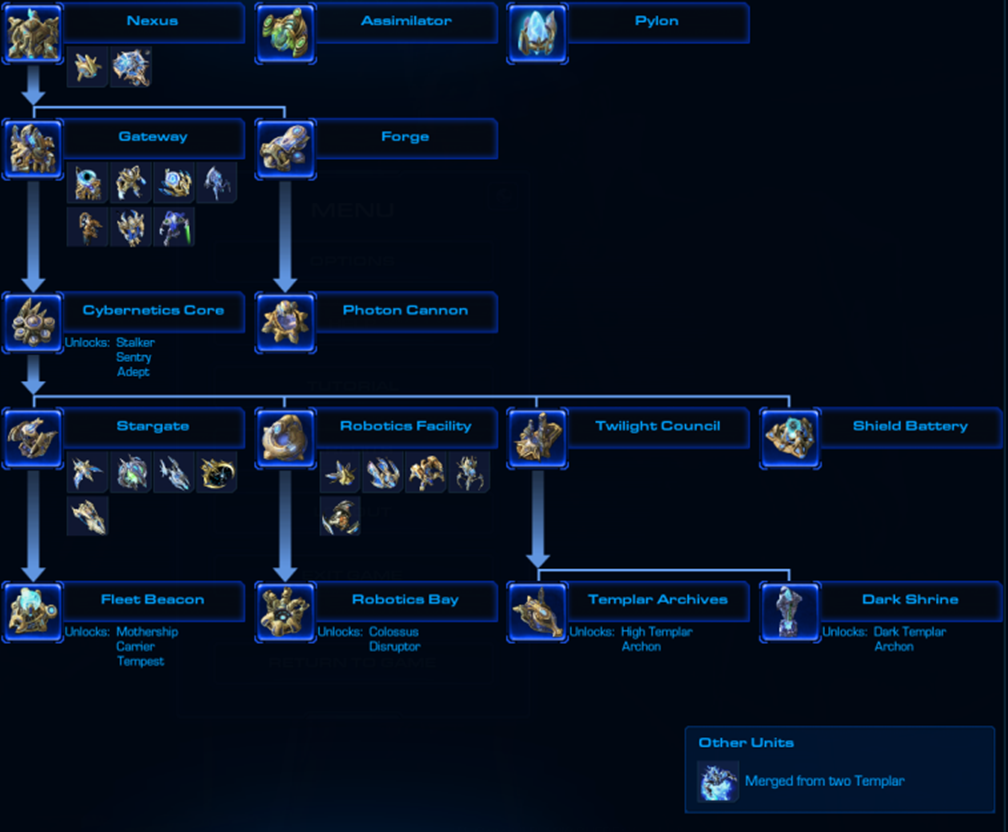
For example, you need a production building "Gate" and a technological building "Cybernetic core" to "Build a combat unit Stalker". If you let the environment perform an action without meeting the conditions, it will not perform anything. The problem is aggravated by the fact, that a partial climb up the technological tree, may not promise rewards, while a full pass can be very beneficial. We can use a mask to nullify the probabilities of actions for which technological conditions are not met. But in this case, a small probability of some actions can cut off an entire technological branch. It is very likely that the agent performs only a narrow set of actions that are available only at the beginning of the game.
I propose to allow actions for which the conditions are not yet met, and to recursively fulfill the technological requirements for this action.
Another problem is that some activities (such as building construction, hiring combat and working units, etc.) require resources. What happens is that an untrained agent quickly sorts through all the actions, and when resources appear for the cheapest action, the agent spends all the resources on it. Thus, the gent does not manage to perform a resource-consuming action, although it can give a game advantage. Often, the agent cannot get out of such a trap. I propose to temporarily freeze the selected action for which there are not enough resources.
For each option, let's launch an untrained agent against the weakest bot to assess the environment exploration quality. We will asses the agents success in covering the technology tree.
1. Default: If the conditions for the activity are not met, the agent skips the action.
In this case, there will be 70% technological tree coverage for a total of 5 games and 55% coverage on average for each of the games.
2. If the conditions for the action are not met, then the probability of selecting this action is 0.
In this case, there will be 50% technological tree coverage for a total of 5 games and 41% coverage on average for each of the games.
3. Use the dependency tree and reservations.
In this case, there will be 82% technological tree coverage for a total of 5 games and 64% coverage on average for each of the games.
In the first case, the agent misses a lot of actions and accumulates abundant resources. On one hand, this allows performing expensive actions, on the other hand, agent is inactive most of the time, which does not allow it to train against more powerful bots.
In the second case, the agent does a lot of cheap actions, and does a poor job on accumulating resources for expensive ones.
Reward Problem
The reward is very dispersed and very poorly reflects the actions’ worth. Given the complexity of the environment, it is almost impossible to learn from such an award, which was shown by DeepMind back in 2017. This is confirmed by my own experiments. In this case, the award is either replaced or mixed with a custom award. Starcraft II has statistics on which you can construct your reward function. As a result of a lengthy selection of coefficients and hyperparameters optimization, you can train the agent against bots with the following statistics.
| AI | Lose | Draw | Win |
|---|---|---|---|
| very_easy | 0 | 5 | 5 |
| easy | 5 | 3 | 2 |
| medium | 9 | 1 | 0 |
| medium_hard | 10 | 0 | 0 |
It was necessary to experiment with the distribution of the reward function to solve this problem.
Let’s formalize the victory conditions: the player who has buildings wins the opponents who do not. The formula can be rewritten as follows:

Let’s convert the formula into something that can be maximized. The second part of the formula can be rewritten as follows:

The first part of the formula is not so easy to convert. It is a bad idea to directly maximize the buildings’ value. But from experience we can draw, that if the player's army is larger than the army of the enemy, then, most likely, the enemy will not be able to destroy the buildings of the player.

As a result:


As a result, we get a logical formula. With a large army, there will be fewer casualties and more destroyed enemies, and getting a large army will require a lot of resources and many producing buildings. But how to transfer the reward for production, the destruction of enemies and the penalty for the loss of the army down the entire technological, economic and production chain?
Let each unit know the beginning and the end of its life. The reward for destroying an enemy unit is distributed to all combat units, taking into account their value, if they are alive at that moment.
Let’s build a dependency graph for each combat unit. To build a combat unit, you may need: a production building, a technological building, minerals, gas, limit. For the manufacturing building and technological building, resources are also needed, and they can also have technological requirements.
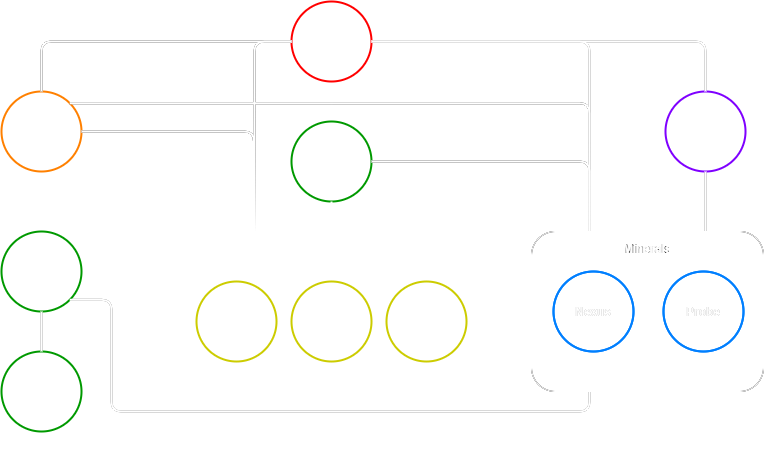
Thus, for each combat unit, you can build a tree if all the dependencies are transferred to its root.
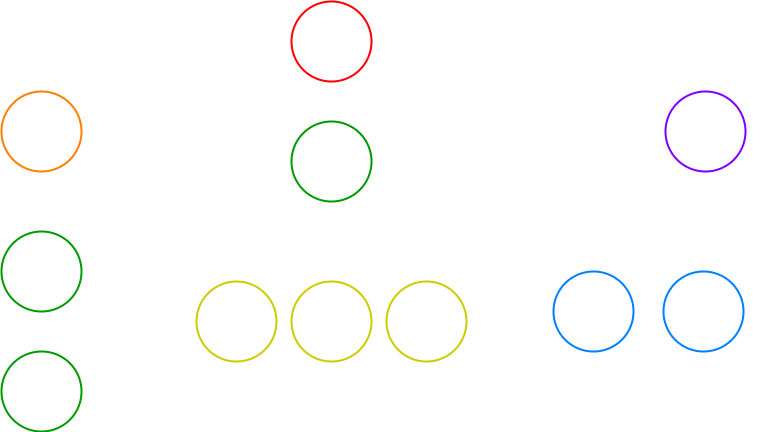
Therefore, when receiving a reward, each combat unit looks at the moment of its creation, and at all its dependencies that were alive at that moment, and partially distributes the reward down the tree.
But we need three more rules to make it work.
- The first: units cannot receive rewards greater than their own value. If there is an unspent reward at a particular moment of time, then it is given for a competent management.
- The second: non-combat units of the same type, except for technological ones, receive awards in turns, with a high priority for those who were built first. It is done to prevent overproduction of workers and producing buildings. In technological buildings, only the first living building receives the award. If its reward is complete, it means that the award remains at the time of its receipt and does not pass to the next technological building of this type. This is done for the same reason.
- The third: let a certain constant be taken away at any given time, so that the agent tries to finish the game faster. This is a very common trick.
| AI | Lose | Draw | Win |
|---|---|---|---|
| very_easy | 0 | 3 | 7 |
| easy | 3 | 4 | 3 |
| medium | 7 | 2 | 1 |
| medium_hard | 9 | 1 | 0 |
Benefits and Rewards
An Advantage can be defined as an improvement measurement from moving from the current state (relative to other available states) by taking a certain action. To do this, we use the rewards that we take from the trajectory, and the assessments of the states that we take from the critic. With the help of these rewards, you can calculate what advantage is obtained when performing the selected action. Thus, even an action that itself did not bring a reward, but brought the state to a favorable position, will receive a positive advantage.
There are different ways to calculate the benefits, we will use the Generalized Advantage Estimation algorithm.
First, the benefit’s generalized evaluation vector GAE is initialized by zeros.
GAE=0
After that, the difference between the assessment of the current state and its purpose is calculated. State assessments are given by the critic.
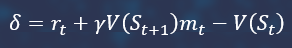
Next, the GAE vector is calculated iteratively, starting with the last state in the trajectory.
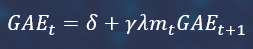
Advantages are calculated this way.
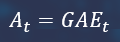
Use the following formula to get state assessments goals.

During the training, you can calculate several awards, each responsible for its own direction. For example, let us have awards responsible for the economy, for the army and for winning the match. Maximizing the reward for the economy is the easiest, since it just needs to put additional bases and produce workers; maximizing match victories is much more difficult. I propose to have a critic for each award, who will evaluate the state, and sum up all the reward's advantages with certain coefficients that will change in the course of the training. For example, at the beginning of the training, make the economy coefficient large, and reduce it with each iteration.
Learning Algorithm
The agent's purpose in reinforcement learning is to maximize the expected reward when following the π policy. Like any machine learning task, we define a set of parameters Θ (for example, the weight of the neural network) to parameterize this policy – π - Θ.
The gradient descent approach is used to solving this problem with the help of neural networks. To do this, we will write a mathematical expectation, and produce a log derivative trick inside the integral.
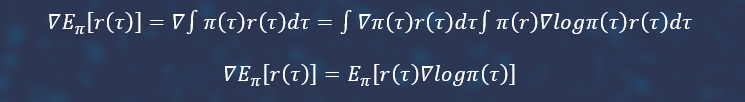
The direct maximization of the previous Monte Carlo formula is called the Reinforce algorithm. But the model does not converge because of the complexity of this task and the large variance.
A more advanced way is to use a Proximal Policy Optimization (PPO), which has a slightly different approach. Trust regions is the cornerstone of the proximal policy optimization. In simple terms, policies do not differ much within the same region. Divergence or plausibility ratio can be taken as a difference measurement. In one iteration of the PPO algorithm, we try to ensure that the policy remains within the region. After that, on the next iteration, the search takes place in a new region.
At the time of the game playing, we will maintain not only the state/action/reward, but also the plausibility and state assessment with the marks old.
The attitude of plausibility during training to plausibility at the moment of playing the trajectory is necessary to prevent policies from getting out of the trust region.
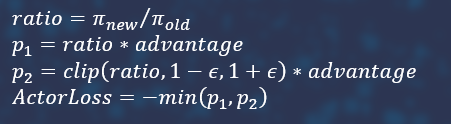
We will also try to ensure that there are no explosive changes in the critic between iterations. To do this, we will monitor the difference between state assessments during training and during the trajectory.
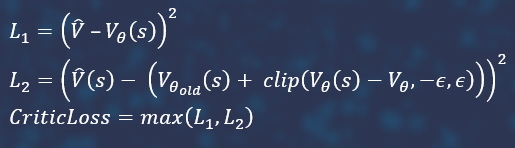
The Total Loss function consists of the critic loss function, the policy loss function and entropy with a negative and a small negative coefficient modulo.

You can try to improve convergence by introducing a kind of advisor. In the case the Total Loss function considers the action unsuccessful, then, it is possible not only to reduce its probability, but also to increase the probability of another, presumably useful, action. This supposedly useful action can be taken from another neural network, which we will train in parallel on the same states, but with some noise. Let's call this neural network an advisor, the main one an actor.
As with PPO, you need to use a plausibility relationship, but the policy loss function is different this time.

The mask is responsible for the fact that the plausibility is within the trust region. At the same time, the critic remains the same, since the same critic will be used for the adviser and for the actor.
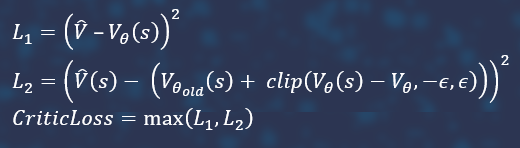
The main difference between the policy of the adviser and the main policy is the function of losses.

The final loss function:

Experiments were conducted in different environments where the advisor helped to improve the PPO results, but this required selecting a coefficient for divergence.
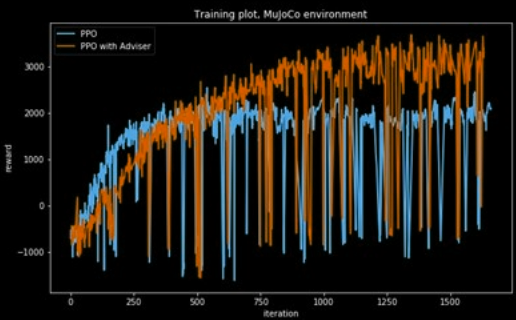
Conclusion
Thanks to such simple hacks, it is possible to train a bot in a very complex environment on a regular notebook in a relatively short time using only reinforcement training, without the need for huge computational clusters and professional players’ game records.
| Model | Enemy AI | Lose | Draw | Win |
|---|---|---|---|---|
| Simple Reward | very_easy | 0 | 5 | 5 |
| easy | 5 | 3 | 2 | |
| medium | 9 | 1 | 0 | |
| medium_hard | 10 | 0 | 0 | |
| Tree Reward | very_easy | 0 | 2 | 8 |
| easy | 3 | 3 | 4 | |
| medium | 7 | 2 | 1 | |
| medium_hard | 9 | 1 | 0 | |
| Weighted Reward + Adviser | very_easy | 0 | 0 | 10 |
| easy | 1 | 2 | 7 | |
| medium | 4 | 4 | 3 | |
| medium_hard | 8 | 0 | 2 |
On the other hand, you can see how difficult it is, and currently it is much easier to write a scripted bot with much better statistics.
Sources Used in This Research
- Grandmaster level in StarCraft II using multi-agent reinforcement learning
- The StarCraft Multi-Agent Challenge
- On Reinforcement Learning for Full-length Game of StarCraft
- StarCraft II: A New Challenge for Reinforcement Learning
- HIGH-DIMENSIONAL CONTINUOUS CONTROL USING GENERALIZED ADVANTAGE ESTIMATION
- Proximal Policy Optimization Algorithms



 Mikalai Pechaneu
Mikalai Pechaneu



